Author: seanhn

Exploit Necromancy in TCMalloc – Reviving the 4-to-N Byte Overflow Primitive with Insert to FreeList[X]

seanhn2 Comments

A couple of months back while looking into a heap overflow in Chrome* I found myself poking around in the internals of TCMalloc. What I found there was pretty interesting. Perhaps the implementers have been watching Twitter and decided to take a proactive approach to security researchers moaning about the difficulties of modern heap exploitation. Maybe they just got caught up in making a blazing fast allocator and couldn’t bring themselves to slow it down with nasty things like integrity checks. Either way, TCMalloc provides a cosy environment for heap exploits to thrive and is worth fully exploring to discover the possibilities it provides.

At Infiltrate next weekend, Agustin Gianni and I will be discussing (among other things) TCMalloc from the point of view of exploitation. Essentially our research into TCMalloc wasn’t so much ‘research’ as it was vulnerability necromancy. In the name of speed TCMalloc has forsaken almost any type of sanity checks you might think of. There are annoyances of course but they are artefacts of the algorithms rather than coherent attempts to detect corruption and prevent exploitation. As a result we can revive a number of primitives from heap exploits past as well as some unique to TCMalloc.

Like most custom allocators, TCMalloc operates by requesting large chunks of memory from the operating system via mmap, sbrk or VirtualAlloc and then uses its own methods to manage these chunks on calls to malloc, free, new, delete etc. Agustin wrote a high level overview here and Google’s project page is also useful for gaining a general idea of its workings. In this post I’m not going to go into the exact details of how the memory is managed (come see our presentation for that!) but instead briefly discuss how thread local free lists function and one useful exploit primitive we gain from it.

ThreadCache FreeList allocation
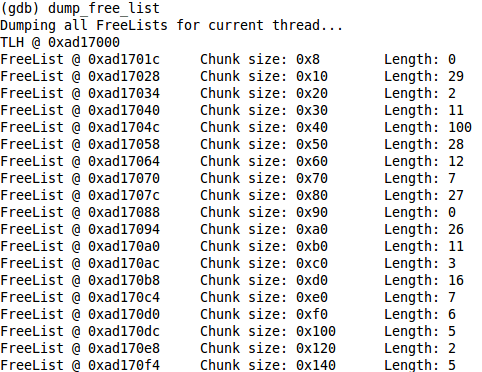
The front end allocator for TCMalloc (with TC standing for ThreadCache) consists of kNumClasses** per-thread free lists for allocations of size < 32768. The FreeLists store chunks of the same size. The bucket sizes are generated in SizeMap::Init and allocations that don’t map directly to a bucket size are simply rounded up to the next size. For allocations larger than 32768 the front end allocator is the PageHeap which stores Spans (runs of contiguous pages) and is not thread specific. The following code shows the interface to the allocator through a call to malloc***.

3604 static ALWAYS_INLINE void* do_malloc(size_t size) {
3605   void* ret = NULL;
3606 
...
3611   // The following call forces module initialization
3612   TCMalloc_ThreadCache* heap = TCMalloc_ThreadCache::GetCache();
...
3621   if (size > kMaxSize) {
3622     // Use page-level allocator
3623     SpinLockHolder h(&pageheap_lock);
3624     Span* span = pageheap->New(pages(size));
3625     if (span != NULL) {
3626       ret = SpanToMallocResult(span);
3627     }
3628   } else {
3629     // The common case, and also the simplest.  This just pops the
3630     // size-appropriate freelist, afer replenishing it if it's empty.
3631     ret = CheckedMallocResult(heap->Allocate(size));
3632   }
...

At line 3612 the ThreadCache pointer for the current thread is retrieved. This object contains a number of thread specific details but the one we are interested in is the FreeList array. A FreeList object contains some metadata and a singly-linked list of free chunks that are managed by very simple primitives such as SLL_Pop, SLL_Push etc. If the allocation size is less than 32768 then the following code is called to retrieve a chunk of the required size.

2888 ALWAYS_INLINE void* TCMalloc_ThreadCache::Allocate(size_t size) {
2889   ASSERT(size <= kMaxSize);
2890   const size_t cl = SizeClass(size);
2891   FreeList* list = &list_[cl];
2892   size_t allocationSize = ByteSizeForClass(cl);
2893   if (list->empty()) {
...
2896   }
2897   size_ -= allocationSize;
2898   return list->Pop();
2899 }

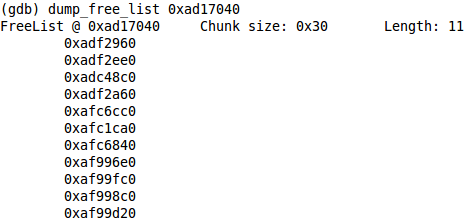
The correct FreeList is retrieved at line 2891 and presuming that it is not empty we retrieve a chunk by calling the Pop method. This results in a call to SLL_Pop with the address of the pointer to the head of the free list.

 761 static inline void *SLL_Next(void *t) {
 762   return *(reinterpret_cast(t));
 763 }
...
 774 static inline void *SLL_Pop(void **list) {
 775   void *result = *list;
 776   *list = SLL_Next(*list);
 777   return result;
 778 }

Insert to FreeList[X] – Reviving the 4-to-N byte Overflow Primitive
The effect of SLL_Pop is through SLL_Next to follow the list head pointer and retrieve the DWORD there and then make that the new list head. Notice there are no checks of any kind on the value of the *list pointer. When I first saw a crash within TCMalloc it was at line 762 in the SLL_Next function. The value of t was 0x41414141 which I had previously overflowed an allocated chunk with. What this means is that on that call to SLL_Pop the list head was an address that I controlled. How could this happen? Consider the following FreeList layout:

FreeList example

The above FreeList has 3 chunks. For simplicity assume that the addresses of A and B are contiguous****. On the first call to malloc chunk A is returned to the application.

FreeList allocation

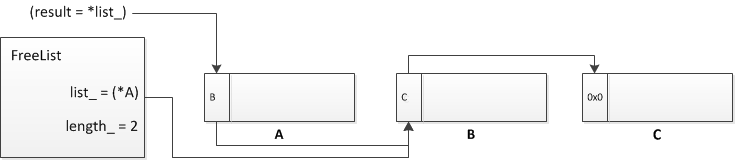
Assume an overflow then occurs when the application writes data to A and B is partially corrupted.

Overflow of Chunk A into Chunk B

The first DWORD of B is the pointer to the next chunk in the FreeList and so we have corrupted the singly-linked list. The first chunk is now B and, as we control the first DWORD of this chunk, we control what the next chunk in the FreeList will be. The chunk C is effectively no longer part of the FreeList. The next allocation of this size will then return the chunk B (presuming no free calls on chunks of this size, within this thread, have occured. Free chunks are prepended to the head of the list) and it will give us control of the list head pointer when *list = SLL_Next(*list) executes.

Allocation from a corrupted FreeList

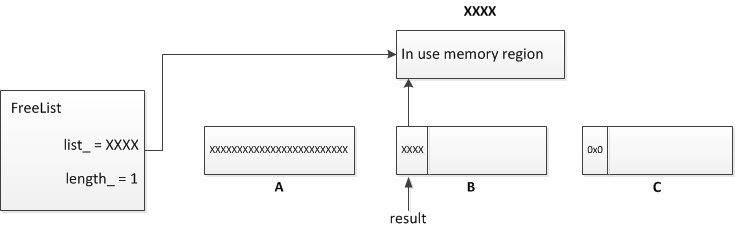
As we control the DWORD at **list we control what the new list head is. In my initial TCMalloc crash this set the list head to 0x41414141. One more allocation of this size will then call SLL_Pop with a controlled list head pointer. The crash I encountered was when SLL_Next attempted to read the next pointer at 0x41414141.

The important part of all this is that by controlling the list head pointer we control the address of the chunk returned and can give back any usable memory region we want to the application. So after one more allocation the situation is as follows:

A memory region of our choosing is handed back to the application

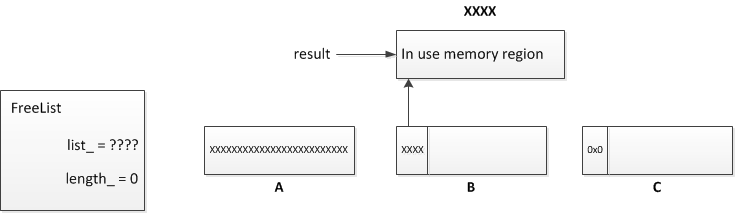
The result of this allocation is a pointer which we control. It is important to note that the first DWORD at this address then becomes the new list head. For a clean exploit it is desirable for either this to be 0x0 or the FreeList list length_ attribute to be 0 after returning our controlled pointer. If we cannot force either of these conditions then future allocations of this size will follow this DWORD, which may not be under our control, and may result in instability in the program before we gain code execution. Another point to note is that if a free call occurs on a pointer that has not previously been noted by TCMalloc as part of a memory region under its control then it will raise an exception that will likely terminate the program. This is important to keep in mind if the memory location we are inserting into the free list is not controlled by TCMalloc. If this is the case then we have to prevent this address from being passed to free before we gain control of the programs execution.

To gain code execution from this primitive it is necessary to find the address of some useful structure to hand back to the application and then have it overwrite that structure with data that we control. For modern systems this will require a memory leak of some kind to find such an address reliably (although heap spraying of useful objects might be an interesting alternative if we can write over one of these objects and then trigger a call through a function pointer or something similar). Despite this requirement, we have a functioning exploit primitive from a heap overflow and one that has not required us to deal with any heap integrity checks or protections. This is not a bad place to be in given the effort that has gone into securing the default allocators for most operating systems.The primitive basically gives the same effect as the Insert to Lookaside technique that was popular on Windows XP but has since been killed on Windows Vista and 7.

Conclusion
In this post I’ve given a quick overview of how we can convert a 4-byte overflow into one that overflows N bytes in an application using TCMalloc. This type of technique has been seen in various places in the past, most notably when overflowing chunks in the Windows XP Lookaside list. It has been largely killed elsewhere but due to the lack of integrity checks in TCMalloc it lives on in a relatively easy to use fashion.

At Infiltrate Agustin and I will discuss a variety of topics related to exploiting WebKit and TCMalloc in much greater detail. The Insert to FreeList[X] technique is but one example of a simple and old heap exploitation tactic that has been revived. Many other exploitation vectors exist and with a grasp of how the allocator works the possibilities are interesting and varied. In our presentation we will describe some of these techniques and also the details of how TCMalloc manages the processes of allocation and deallocation such as is relevant to manipulating the heap for exploitation.


* TCMalloc is not the allocator used by the Chrome Javascript engine V8. That has its own allocator that can be found in the src/v8/src/ directory of the Chrome source. Have a look at spaces.[cc|h] and platform_X.cc to get started.
** For WebKit in Safari kNumClasses is 68 but for Chrome it is 61. There seem to be some other differences between the various uses of TCMalloc and are worth keeping in mind. For example, in Chrome the maximum free list length is 8192 whereas in Safari is is 256.
*** We’re looking at the TCMalloc code embedded in WebKit revision 79746 Source/JavaScriptCore/wtf/FastMalloc.cpp. It’s effectively the same as that in the Chrome release and elsewhere, modulo the previous point.
**** FreeLists are created from Spans which are contiguous pages in memory that get subdivided to give the FreeList chunks. The chunks are prepended to the list during creation though so they end up in reverse address order. This means that if A, B are two contiguous addresses then the FreeList will initially be ordered as B -> A. In order to get the desired ordering we need to rearrange the fresh FreeList by allocating B, allocating A, free’ing B and then free’ing A. This will result in the ordering A -> B and another allocation from this FreeList will give back the address A.

Heap Scripts for TCMalloc with GDB’s Python API

seanhn4 Comments

When writing heap exploits it’s necessary to be able to view the heap state during debugging. As part of our work on TCMalloc, Agustin and I have written up some heap scripts for Immunity Debugger and GDB that make the process of tracking what TCMalloc is up to quite easy. There are quite a few scripts that do similar things for ID and different heap implementations so in this post I’m going to focus on the GDB side of things. Recent versions of GDB contain an embedded Python interpreter that provides easy access to the internals of an application being debugged. Being able to write scripts in Python to automate debugging tasks is really useful and hopefully the GDB guys will maintain the project.

The scripts I will be discussing in this post can be found here. Copy the gdbinit file your home directory or the one where you will be launching gdb from and rename it to .gdbinit. Modify the pyscripts_dir variable to point to the directory where you extracted the scripts. To load the commands run source /path/to/scripts/dump_free_list.py or source /path/to/scripts/search_free_lists.py. This will make the commands dump_free_list and search_free_lists available within gdb.

The data structures used by TCMalloc are relatively simple so the scripts have little to do besides reading memory and walking lists. Each thread in an application using TCMalloc has its own TCMalloc_ThreadCache object which contains information on the FreeLists for that specific thread. The FreeLists themselves are ThreadCache_FreeList objects, each of which contains a list_ attribute that points to the head of a singly linked list of free chunks. We can access the TLS for a given thread via pthread_self() in GDB and find the ThreadCache_FreeList pointer at the offset -4 from there. The file tcmalloc.py contains abstractions for the ThreadCache_FreeList and TCMalloc_ThreadCache structures. In dump_free_lists.py we can see the initialisation of the ThreadCache abstraction via the following code:

 24         tls = gdb.parse_and_eval("pthread_self()")
 25         # threadlocal_heap is at TLS - 4
 26         threadlocal_heap = buf_to_le(
 27             self.cur_proc.read_memory(tls - 4, DWORD_SIZE))
 28 
 29         tc = ThreadCache(self.cur_proc, threadlocal_heap)

The ThreadCache instance then provides access to the FreeLists for the current thread through getFreeLists. The size classes that TCMalloc uses to bucket chunks together for allocations less than 32768 in size are generated at run-time. To view them run tcmalloc.py outside of gdb with no arguments.

The number of size classes, and hence the number of FreeLists per thread, is dependent a constant that may change between applications embedding TCMalloc. For Chrome it is 61 and hence we have 61 different FreeLists per thread. If we run dump_free_lists within gdb with no arguments it will dump all free lists, their lengths and the chunk size that list is responsible for.

TCMalloc FreeLists within Chrome on Linux

The getFreeLists function will return each of these FreeLists as a FreeList object. This object contains a list_ptr attribute that corresponds to the list_ pointer found in the TCMalloc source for each FreeList. It points to a singly linked list of free chunks that we can iterate over using the getChunks function of a FreeList object.

If we run dump_free_lists with one or more space separated addresses it will treat them as pointers to ThreadCache_FreeList structures and dump them accordingly.

The chunks in a given FreeList

The scripts archive also contains the search_free_lists command which will search the FreeLists to see if an address lies within a chunk on any of the FreeLists. After Infiltrate we will release the rest of the scripts for ID and GDB but these should be enough to get you started with TCMalloc and GDBs Python API.

Misleading the Public for Fun and Profit

seanhn14 Comments

Sometimes I read a research paper, usually in the area where computer science meets application, and it’s obvious that the authors are far overstating the practical impact of the work. This can be due to the researchers simply not having any exposure to the practical side of the field in which they are investigating and thus accidentally (through ignorance) overstate their claims. Alternatively it can be a purposeful and deliberate attempt to mislead and posture in front of a readership that hopefully won’t know any better.

The first case is presumably simple ignorance but is still lamentable. The obvious solution here is to avoid making such claims at all. If the research cannot stand on its own then perhaps it is not worthwhile? Researchers (both academic and industrial) have a habit of jumping on problems they underestimate, throwing a variety of techniques at them, hoping one sticks and then calling the problem solved. This typically occurs when they are not actually required to solve the problem correctly and robustly but merely as a ‘prototype’. They then get pilloried by anyone who actually has to solve the problem properly and almost always because of a disparity between claims made and the real impact rather than issues with methodology, recording or technical aspects.

The second case is far more insidious and unfortunately I think not uncommon. In academic research it can be easy to impress by combining cutting edge, but not necessarily original, research with a practical problem, sort-of solving parts of it and like before declaring it solved. Often followed quickly by phrases involving ‘game changing’, ‘paradigm shifting’ and so forth. Personally, I think this is a serious problem in the research areas that are less theoretical and more practical. Often the investigators refuse to accept they aren’t actually aware of the true nature of the problem they are dealing with or how it occurs in the real world. Egotistically this is difficult as they are often lauded by their academic peers and therefore surely must grasp the trivialities of the practical world, no? At this point a mixture of ego, need to impress and lack of ethics combine to give us papers that are at best deluded and at worst downright wrong.

Regardless of whether a paper ends up making such claims mistakenly for the first or the second reason the result is the same. It cheapens the actual value of the research, results in a general loss of respect for the capabilities of academia, deludes the researchers further and causes general confusion as to where research efforts should be focused. Worse still is when attempts to overstate the impact are believed by both the media and other researchers resulting in a complete distortion between the actual practical and theoretical value of the research and it’s perceived impact.

Now, on to the paper that has reminded me of this most recently: The latest paper from David Brumleys group at CMU titled “AEG: Automatic Exploit Generation“. I was looking forward to reading this paper as it was the area I worked on during my thesis but quite honestly it’s incredibly disappointing at best and has serious factual issues at worst. For now let’s focus on the topic at hand ‘overstating the impact of academic research cheapens it and spreads misinformation‘. With the original Patch-Based Exploit Generation paper we had all sorts of stories about how it would change the way in which patches had to be distributed, how attackers would be pushing buttons to generate their exploits in no time at all and in general how the world was about to end. Naturally none of this happened and people continued to use PatchDiff. Unfortunately this is more of the same.

Near the beginning of the most recent paper we have the following claim “Our automatic exploit generation techniques have several immediate security implications. First, practical AEG fundamentally changes the perceived capabilities of attackers“. This statement is fundamentally flawed. It assumes that practical AEG is currently possible on bugs that people actually care about. This is patently false. I’ve written one of these systems. Did it generate exploits? Yes it did. Is it going to pop any program running on a modern operating system with the kinds of vulnerabilities we typically see? Nope. That would require at a minimum another 2 years of development and at that point I would expect a system that is usable by a skilled exploit writer as an augmentation of his skillset rather than a replacement. The few times I did use the tool I built for real exploits it was in this context rather than full blown exploit generation. The system discussed in the mentioned paper has more bells and whistles in some areas and is more primitive in others and it is still an unfathomable distance from having any impact on a realistic threat model.

Moving on, “For example, previously it has been believed that it is relatively difficult for untrained attackers to find novel vulnerabilities and create zero-day exploits. Our research shows this assumption is unfounded“. It’s at this point the distance between the authors of this paper and the realities of industrial/government/military vulnerability detection and exploit development can be seen. Who are the people we are to believe have this view? I would assume the authors themselves do and then extrapolated to the general exploit creating/consuming community. This is an egotistical flaw that has been displayed in many forays by academia into the vulnerability detection/exploit generation world.

Let’s discuss this in two parts. Firstly, in the context of the exploits discussed in this paper and secondly in the context of exploits seen in the real world.

In the case of the bug classes considered in the paper this view is entirely incorrect. Anyone who looks at Full Disclosure can regularly see low hanging bugs being fuzzed and exploited in a cookie cutter style. Fuzz the bug, overwrite the SEH chain, find your trampoline, jump to your shellcode bla bla bla rinse and repeat, start a leet h4x0r group and flood Exploit DB. All good fun, no useful research dollars wasted. The bugs found and exploited by the system described are of that quality. Low hanging, fuzzable fruit. The ‘training’ involved here is no more than would be required to set up, install and debug whatever issues come up in the course of running the AEG tool. In our most basic class at Immunity I’ve seen people who’ve never seen a debugger before writing exploits of this quality in a couple of days.

For more complex vulnerabilities and exploits that require a skilled attacker this AEG system doesn’t change the threat model. It simply doesn’t apply. A fully functional AEG tool that I can point at Firefox and press the ‘hack’ button (or any tool that had some sort of impact on real threats. I’d be happy with exploit assistance rather than exploit generation as long as it works) would of course, but we are a long, long way from that. This is not to say we won’t get there or that this paper isn’t a step in the right direction but making the claim now is simply laughable. To me it just reeks of a research group desperate to shout ‘FIRST!’ and ignoring the real issues.

A few more choice phrases for your viewing pleasure:

“Automated exploit generation can be fed into signature generation algorithms by defenders without requiring real-life attacks” – Fiction again. This would be possible *if* one had a usable AEG system. The word I presume they are looking for is *could*, “could be fed into”.

“In order to extend AEG to handle heap-based overflows we would need to also consider heap management structures, which is a straight-forward extension” – Again, this displays a fundamental ignorance of what has been required to write a heap exploit for the past six or so years. I presume they heard about the unlink() technique and investigated no further. Automatic exploit generation of heap exploits requires one to be able to discover and trigger heap manipulation primitives as well as whatever else must be done. This is a difficult problem to solve automatically and one that is completely ignored.

In reference to overflows that smash local variables and arguments that are dereferenced before the function returns and therefore must be valid – “If there is not enough space to place the payload before the return address, AEG can still generate an exploit by applying stack restoration, where the local variables and function arguments are overwritten, but we impose constraints that their values should remain unchanged. To do so, AEG again relies on our dynamic analysis component to retrieve the runtime values of the local variables and arguments” – It’s at this point that I start to wonder if anyone even reviewed this thing. In any program with some amount of heap non-determinism, through normal behaviour or heap base randomisation, this statement makes no sense. Any pointers to heap allocated data passed as arguments or stored as local variables will be entirely different. You may be lucky and end up with that pointer being in an allocated heap region but the chances of it pointing to the same object are rather slim in general. Even in the context of local exploits where you have much more information on heap bases etc. this statement trivialises many problems that will be encountered.

Conclusion

With the above paper I have two main issues. One is with the correctness of some of the technical statements made and the other is with distortion between reality and the stated impact and generality of the work. For the technical issues I think the simple observation that they are there is enough to highlight the problem. The flawed statements on impact and generality are more problematic as they display a fundamental corruption of what a scientific paper should be.

I have a deep respect for scientific research and the ideals that I believe it should embody. Much of this research is done by university research groups and some of the papers produced in the last century are among humanities greatest intellectual achievements. Not all papers can be revolutionary of course but even those that aren’t should aim to uphold a level of scientific decorum so that they may contribute to the sum of our knowledge. In my opinion this single idea should be at the heart of any university researcher being funded to perform scientific investigation. A researcher is not a journalist nor a politician and their papers should not be opinion pieces or designed to promote themselves at the expense of facts. There is nothing wrong with discussing perceived impact of a paper within the paper itself but these statements should be subjected to the same scientific rigour that the theoretical content of the paper is. If one finds themselves unqualified (as in the above paper) to make such statements then they should be excluded. Facts are all that matter in a scientific paper, distorting them through ignorance is incompetence, distorting them on purpose is unethical and corrupt.

Augment your Auditing with a Theorem Prover

seanhn2 Comments

A better post title may have been ‘Outsourcing your thinking when lack of sleep makes basic arithmetic difficult’. Anyways, consider the following code from the  ArrayBuffer::tryAllocate function found in WebCore/html/canvas/ArrayBuffer.cpp.

85	void* ArrayBuffer::tryAllocate(unsigned numElements, unsigned elementByteSize)
86	{
87	    void* result;
88	    // Do not allow 32-bit overflow of the total size
89	    if (numElements) {
90	        unsigned totalSize = numElements * elementByteSize;
91	        if (totalSize / numElements != elementByteSize)
92	            return 0;
93	    }
94	    if (WTF::tryFastCalloc(numElements, elementByteSize).getValue(result))
95	        return result;
96	    return 0;
97	}

 

Lets ignore for now whether or not you know that the check on line 91 is valid or not. For the sake of argument, assume you’re unsure about whether this code does in fact prevent a situation where totalSize can overflow and the allocation function on line 94 can still get called. In such a situation you could try and reason through on paper whether the check is safe or not, but this is potentially error prone. The other option is to model the code and throw a theorem prover at it. The advantage of this approach is that if the code is safe then you end up with a proof of that fact, while if it’s unsafe you end up with a set of inputs that violate the safety check.

The following is my model of the above code:

[sean@sean-laptop bin]$ cat test.smt
(benchmark uint_ovf
:status unknown
:logic QF_BV

:extrafuns ((totalSize BitVec[32])(numElements BitVec[32])(elSize BitVec[32]))
:extrafuns ((a BitVec[64])(b BitVec[64])(big32 BitVec[64]))

; if (numElements) {
:assumption (bvugt numElements bv0[32])

; unsigned totalSize = numElements * elementByteSize;
:assumption (= totalSize (bvmul numElements elSize))

; totalSize / numElements != elementByteSize
:assumption (= elSize (bvudiv totalSize numElements))

; Check if an overflow is possible in the presence of the 
; above conditions
:assumption (= big32 bv4294967295[64])
:assumption (= a (zero_extend[32] numElements))
:assumption (= b (zero_extend[32] elSize))
:formula (bvugt (bvmul a b) big32)
)

 

(The above .smt file is in SMTLIB format. Further information can be found at [1], [2] and [3])
The above models tryAllocate pretty much exactly. The final three assumptions and the formula are used to check if the integer overflow can occur. Mixing bitvectors of different types isn’t allowed for most operations so it is necessary first to extend numElements and elSize into 64 bit variables. We then check for overflow by multiplying these 64 bit extensions by each other and checking if the result can be greater than 0xffffffff (big32) while also satisfying the conditions imposed in modelling the function.

[sean@sean-laptop bin]$ ./yices -V
Yices 2.0 prototype. Copyright SRI International, 2009
GMP 4.3.1. Copyright Free Software Foundation, Inc.
Build date: Fri Apr 23 11:15:16 PDT 2010
Platform: x86_64-unknown-linux-gnu (static)
[sean@sean-laptop bin]$ time ./yices -f < test.smt 
unsat

real	0m0.587s
user	0m0.576s
sys	0m0.008s

 

And there we have it, our proof of safety (modulo modelling errors on my behalf and implementation errors in yices). Given the assumptions specified it is not possible for the multiplication at line 90 to overflow and still satisfy the condition at line 91. Total time from starting modelling to a proof, about 10 minutes.

[1] Logic for quantifier free bit-vector logic
[2] Theory for fixed size bit-vectors
[3] SMT-LIB v2 reference

Edit: I modified the above formula and some of the text after noticing an error. Hence any comments below may refer to an older version of the post.

Code Analysis Carpentry (Ruxcon 2010)

seanhn1 Comment

Ruxcon is next month and I’ll be giving a talk titled Code Analysis Carpentry (Or how not to brain yourself when handed an SMT solving hammer). Here’s the abstract:


This talk will be one part “Oh look what we can do when we have a Python API for converting code into equations and solving them” and one part “Here’s why the world falls apart when we try to attack every problem in this way”.

One popular method of automated reasoning in the past few years has been to build equational representations of code paths and then using an SMT solver resolve queries about their semantics. In this talk we will look at a number of problems that seem amenable to this type of analysis, including finding ROP gadgets, discovering variable ranges, searching for bugs resulting from arithmetic flaws, filtering valid paths, generating program inputs to trigger code and so on.

At their core many of these problems appear similar when looked at down the barrel of an SMT solver. On closer examination certain quirks divide them into those which are perfectly suited to such an approach and those that have to be beaten into submission, often with only a certain subset of the problem being solvable. Our goal will be to discover what problem attributes place them in each class by walking through implemented solutions for many of the tasks. Along the way the capabilities and limitations of the modern crop of SMT solvers will become apparent. We will conclude by mentioning some other techniques from static analysis that can be used alongside a SMT solver to complement it’s capabilities and alleviate some of the difficulties encountered.

The schedule is full of talks that look like fun. I’m really looking forward to seeing a few in particular, especially those by Silvio Cesare, Ben Nagy and kuza55. Looks like it’ll be just as entertaining as REcon (with hopefully not quite as much sun-burn)! Mostly I’m just looking forward to watching 30 people get on stage and try to out do each other with sheep related innuendo. If there isn’t at least one drunken presenter abusing the crowd I’m calling it a failure!

Determining variable ranges (Part I)

seanhn4 Comments

This post is the first of a two part discussion in which we’ll tackle the title problem with some scripts on top of Immunity Debugger 2.0. To begin lets pose the question as follows: ‘Given an output register or memory location v, of width w, and a set of input registers/memory locations (x_0, w_0), …, (x_n-1, w_n-1) what are the possible values for v after the execution of a sequence of n instructions i_0, i_1, … i_n-1‘. Lets call this sequence p representing any concrete path through a program. Before we continue it may be worth your while to think about some solutions to this problem given whatever tools and techniques you think appropriate.

The most primitive solution is probably to just run the code and iterate over all possible combinations of input variables. This will require exactly 2^w_0 * … * 2^w_n-1 runs and with a running time exponential the number of input variables. Presuming we only want to run our variable range analysis on a specific sub-path then for this solution we need a way to snapshot a process and re-run the sub-path multiple times or, if feasible, re-run the entire path and enable the analysis for the required sub-path.

Lets now presume we have at our disposal a method of converting p into a formula F(p) interpretable by an SMT solver that gives the precise semantics of p. Given what we know about SMT solvers one obvious solution to the above problem immediately presents itself. By creating the conjunction of F(p) with a formula expressing v := x for each x in the range 0 to 2^w-1 we can, with 2^w-1 queries of our solver, determine the full range of possible values for v, those x values resulting in a satisfiable formula, as well as the assignments to input variables that result in each value.

How long will this many queries take to run? Naturally this will be a factor of n and the complexity of the instructions in p (due to the relative solving costs for linear vs non-linear arithmetic and so on) but let’s chose an instruction sequence and do some testing. The following instruction sequence was chosen as it is short enough to serve as a good example but arithmetically complex enough that the potential range of values for ESI at 0x76792186 require some manual labour to figure out.

Our tests will be for the range 0x767920c6:76792186

The input variables to this sequence are EDX and ECX and the output variable we are interested in is ESI (although we could of course look for results for any variable written to during this sequence). Now it’s time to start thinking about our algorithm a little more. For certain output values over this instruction sequence our solving code can hit upwards of 6000 queries a minute but doing this 2^32 times is still going to take a prohibitively long time to finish. Not to mention the fact that we’ll want to run this solution on much longer instruction sequences in the future.

The approach I decided to take here was to try to divide the possible output values into ranges and try to weed out entire ranges of unsatisfiable output values at once by constructing queries like v >= LOWER_BOUND AND v <= UPPER_BOUND. If such a formula is satisfiable then we can conclude that within the range LOWER_BOUND:UPPER_BOUND is at least one output value that can be achieved given the correct input.

Effectively this results in a binary search of the output value space. In the best case scenario the largest ranges possible are proven to be unsatisfiable, or in other words no possible output value lies within that range. e.g. If our range is 0:2**32-1 and we split it in two to query the ranges 0:(2**32-1)/2 and (2**32-1)/2 + 1: 2**32-1 and discover that the first range gives an unsatisfiable result then we have immediately removed 2**32/2 potential output values that we may have otherwise had to investigate. The algorithm is essentially:


lower = 0
upper = 2**32 - 1

ranges = [(lower, upper)]
while len(ranges) > 0:
    lower, upper = ranges.pop()
    query = create_range_query(lower, output_register, upper)
    if solver.isSatisfiable(query):
        diff = lower - upper
        if diff <= bucket_size:
            sat_ranges.append((lower, upper))
        else:
            half = diff/2
            ranges.append(lower, lower + half)
            ranges.append(lower + half + 1, upper)

Once this code has run the array sat_ranges contains a list of ranges. In each of these ranges there is at least one valid output value that could potentially end up in v given the correct input values. The larger we set bucket_size the fewer queries we require in this first phase to discover our candidate ranges but the more coarse grained our initial results are. The following screenshot shows an analysis of our earlier code using a bucket size of 32768.

Coarse analysis searching for candidate ranges

1159 queries were required to discover 256 candidate ranges with total run time at 456 seconds. While these results are still far from giving us exact ranges for v (8388352 queries away in fact, which is still far too many to be practical) a definite pattern has emerged in the output values. This pattern is of course an artefact of the logical instructions found in the instruction sequence and we can see quite clearly in the above screen shot all our valid ranges are of the form 0xY4X00000:0xY4X07FFF for all X, Y in [1,..,9]. A quick glance over the instructions involved in the code sequence is enough to indicate that if we can resolve the valid indexes into any of these ranges then the same indexes will be valid for the other ranges.

The script varbounds.py also allows us to specify the initial lower and upper bounds for the ranges so we can use that to investigate a particular range.

Here we check the 0x0x400000:407fff range

Now we’re starting to get somewhere! By setting the bucket size to 256 and querying the range 0x400000:0x407fff we’ve managed to reduce our potential valid results to living within 16 different buckets of size 256. All this with only 37 queries to the solver and a run time of just over a second. The reason for so few queries is essentially that large ranges were proved unsatisfiable meaning we didn’t have to split/investigate their sub-ranges. In order to discover the exact values that are possible within these ranges we need to take one more step; instead of querying ranges we need to query for concrete values within these ranges as initially proposed. The difference now is that we have reduced our untenable 2**32 queries to a mere 4000 or so.

(In the following screenshot the -p option tells the script to use precise queries instead of ranges. The ranges under ** Valid values for ESI ** were constructed by individual queries to the values within these ranges and then merging the ranges after the fact to make the results easier to read)

Discovering the exact values that are possible within the range 0x400000:0x407fff

In the end you can see that we have proven there are exactly 256 possible valid values from that initial large range of size 32768. Precise results required 4133 queries which only took 87 seconds to complete. At this point we can extrapolate our results back to the other ranges and come up with a pattern we know any result in ESI will match. It is 0xY4X4Zc0 to 0xY4X4Zcf for all X, Y, Z in [0,..,9].

A quick test on another range confirms this pattern.

Confirming our byte pattern holds for the other ranges

Improving the above solution with abstract interpretation

So for the above test case the results are pretty cool. It is of course easy to think of examples where blindly applying this technique will result in failure to reduce the initial problem of a large potential output space. Consider any sequence of instructions built purely from arithmetic instructions like add, mul, div etc. In this case the binary search would simply split the full output range into a sequence of bucket sized ranges without actually removing any of them as all values are possible given at least one free input variable.

Another pretty obvious point is that by ignoring the semantics of logical operators we are effectively ignoring an even simpler way to perform the initial filtering. In our solution we blindly convert the initial instruction sequence to equations in our SMT solver and then entirely ignore the original instructions for the remainder of our task. Much like the above case we are losing valuable information in doing so. Take the instruction and eax, 0xffff. If such an instruction appears right before the value in eax is moved into our output register then an analysis with the ability to include information on logical operator semantics could pre-limit its search to values in the 0xffff range. A very simple application of abstract interpretation could drastically reduce the number of cases where we need to go to a solver at all by maintaining information on the state of each bit for each register or memory location in play. With an abstract domain consisting of {MUST_BE_SET, CANT_BE_SET, MIGHT_BE_SET} and abstract versions of and, or, xor etc. we could easily propagate the required information e.g. MUST_BE_SET ^ CANT_BE_SET => CANT_BE_SET, MUST_BE_SET ^ MUST_BE_SET => MUST_BE_SET, MUST_BE_SET ^ MIGHT_BE_SET => MIGHT_BE_SET and so on. I haven’t thought this one through entirely and I’m sure there’s a nicer way to present the theory but merging information gained from abstract interpretation into solutions with SMT solving is, in my opinion, one of the most powerful approaches to program analysis at the moment.

A third instruction category worth considering is conditional jumps. By their nature every conditional jump imposes constraints on the path in which it occurs. If it is taken the positive constraint holds, otherwise its negation holds. Once again it is obvious that by ignoring these constraints at a higher level than SMT equations we risk pointless queries to the solver but I haven’t considered the problem enough to come up with a good lightweight abstract analysis. The emphasis here being on ‘lightweight’ as if the solution is more expensive than running the solver then it isn’t worth it.

Scalability

One interesting question posed to me about this script is ‘How does it compare to simply running the code and iterating over the possible input values?’. The honest answer is that I have no metrics on that approach to compare it with. What I would say however is that practically implementing that kind of solution for longer program paths involving memory accesses is likely to be no walk in the park either. As mentioned earlier, each run in such a solution is going to have to restore a ‘snapshot’ of some kind and will require exactly 2^w_0 * … * 2^w_n-1 iterations. The question then becomes ‘How does the solvers running time scale with the number of input variables and their width?’. Again my answer is really the same in that I haven’t ran enough experiments to come to any valid conclusions yet. I would imagine that in the worst case the scaling is just as bad given the nature of the problem but that the average case is far better. Gathering some decent stats on this is actually my next intended project when I get some free time.

Conclusion

1. If you have a specific question you need answering then dealing with annoying instruction sequences doesn’t have to be a nightmare. Solvers. Use them.
2. Solvers. Don’t use them for everything. There’s a world of other awesome program analysis techniques and tools out there than in many situations complement theorem provers and decision procedures very nicely and in other cases can give far superior results. Also, as in the above situation there’s always room for a healthy amount of human interaction and guidance.

Validity, Satisfiability and Code Semantics

seanhn

In a recent post to DD I mentioned some interesting features that will be available in Immunity Debugger 2.0. These features rely on a translation layer from x86 code to SMT formulae that Pablo constructed as part of his work on DEPLIB 2.0. In the past few weeks I got some time to put together a few scripts for ID that replicate some of the more useful tasks that we can use a solver for. In this post I am going to elaborate on one such script which is designed to find ROP gadgets meeting user specified conditions.

find_gadget.py is a relatively simple piece of software which is a testament to Pablo’s API development, the Python programming language and, I think quite importantly, the suitability of mathematical logic for reasoning about machine code. This final point is of course unsurprising but it provides good motivation when considering the merits of abstracting x86 code to more logical/mathematical representations for analysis.

We begin our gadget search by running gadgets.py. Currently this script finds any instruction sequence ending in a ret instruction (with support for pop REG/jmp REG etc. in the works). This takes about 360 seconds to run on QuickTimeAuthoring.qtx (2.16MB) and finds 80,000 candidate gadgets. For now no further analysis is done on these gadgets but we’re working on some fun stuff in that area.

At this point we can use find_gadget.py to search the candidate gadgets for one that meets whatever semantics we have in mind. For now the semantics are specified via the -d, -n and -v/-s options, i.e. DESTINATION RELATION SOURCE/VALUE. For example, to represent EAX <= [EBX+24] we would use -d EAX -n <= -s [EBX+24]. (This is a little cumbersome and not as flexible as one might like so we built a BNF grammar based on pyparsing that allows for arbitrary semantics to be specified as constraints and that should be swapped in pretty soon.) The full set of arguments are shown in this screenshot:

Arguments to find_gadget.py

Once we have specified our arguments the script gets on with the fun part. Our algorithm is as follows:


for gadget in candidiate_gadgets:
    sa = SequenceAnalyzer(reg_model, flag_model, mem_model) # 1
    sa.analyze(gadget.addr, gadget.depth) # 2
    
    if relation == '=':
         rel_expr = sa.solver.eqExpr(dest, src) # 3
    elif relation == '<=':
         ...

    preserve_expr = None
    if preserve_regs != None: # 4
         for reg in preserve_regs:
              eq_expr = sa.solver.eqExpr(sa.regs_before[reg], sa.regs_after[reg])
              preserve_expr = sa.solver.boolAndExpr(preserveExpr, eq_expr)
        rel_expr = sa.solver.boolAndExpr(rel_expr, preserve_expr)

    res = sa.solver.queryFormula(rel_expr) # 5
    if generic_gadgets_only:
         if res == VALID:
              # VALID GADGET FOUND
     else:
          if res == SATISFIABLE:
              # SATISFIABLE GADGET FOUND

#1 Modelling registers, flags and memory
One of the arguments you may have noticed to the script is -c. This argument tells the script that we want to look for ‘context specific’ gadgets that satisfy our semantics when current values in registers, memory and flags are taken into account. The alternative is to look for generic gadgets that will meet the required semantics regardless of the context e.g. inc eax will only set eax to 0 if it previously contained -1 while xor eax, eax will always set it to zero. We’ll discuss this a little more on point #5.

#2 Gadgets to equations
The main coding effort in building this framework was building a transformer for each x86 instruction into the domain of our theorem prover. This requires one to encode accurately the semantics of the instruction over flags, registers and memory and is the backbone of any tool that reasons about assembly code using a solver. This long and drawn out functionality is hidden behind the analyze function which iterates over each instruction and updates the solver state. Once this has completed our solver internally has an accurate representation of the gadgets semantics in the form of several equations.

# 3 & # 4 Adding our gadget constraints
Once one has a representation of a sequence of instructions as equations the next step is typically to append some further constraints derived from the task at hand and then query the solver to determine if they are valid or satisfiable, and if so, to retrieve an input that makes it so. In our case our constraints simply specify a relation between an output register/memory location and an input register/memory location or a constant. We also allow the user to specify a number of registers that the gadget should preserve. We end up with a formula specifying something like (ESP_after == EAX_before+4 AND EBX_after == EBX_before), which is essentially a stack swap with the buffer pointed to by EAX and preserving the EBX register.

# 5 Context specific vs. generic gadgets
After encoding our constraints as a formula in steps #3 and #4 we can then query the solver to determine the status of these constraints in the context of the gadget encoding constructed in step #2. What do we mean by ‘status’? Well, when considering the SAT problem a formula can either be valid, invalid, satisfiable or unsatisfiable. A formula is satisfiable if there exists an assignment to free variables that makes it true and is unsatisfiable otherwise. A formula is valid if its negation is unsatisfiable or invalid otherwise. In other words, a formula is valid if any variable assignment makes it true. Why is this important? If we’re looking for generic gadgets then we want them to meet our constraints regardless of the context, therefore we leave all memory locations, registers and flags free and require that our constraints are VALID in the context of the gadget. That is, there exists no assignment to the memory locations, registers and flags that would result in the gadget not meeting our constraints.

The next few screenshots show some usage examples.

A generic gadget to set EAX to 1
A generic gadget to set EAX to 1 while preserving ESI
Finding multiple gadgets to achieve the same result

find_gadget.py is a very simple script but at the same time can find some very complicated instruction sequences in a short amount of time. In particular it can find tricky stack swapping gadgets and can process about 200,000 gadgets in 3 hours, which is probably a bit quicker than doing it by hand. In some upcoming posts I’ll elaborate a bit more on what can be done with the x86 -> SMT transformer -> solver code. For an idea of some of the things we’re hoping to implement many of the papers published in the last few years on symbolic execution and derived techniques are a good starting point and quite a few are linked from the Practical Software Verification Wiki

Applying Taint Analysis and Theorem Proving to Exploit Development

seanhn

Last week I spoke at REcon on the above topic. The slides can be found here. The abstract for this talk is as follows:

As reverse engineers and exploit writers we spend much of our time trying to illuminate the relationships between input data, executed paths and the values we see in memory/registers at a later point. This work can often be tedious, especially in the presence of extensive arithmetic/logical modification of input data and complex conditions.

Using recent (and not so recent) advances in run-time instrumentation we can go a long way towards automating the process of tracking input data and its effects on execution. In this talk we will discuss possible approaches to solving this problem through taint analysis. The solutions we will discuss are useful in many scenarios e.g. determining the set of conditional jumps under our control, discovering buffers in memory that are useful for injecting shellcode, tracking parameters to potentially insecure function calls, discovering ‘bad bytes’ for exploits and so on.

Building on this we will delve into the construction of logical formulae expressing the relationships between input and data in memory and ways in which these formulae can be manipulated and solved for interesting results. Depending on how we manipulate the initial formulae we can use theorem provers to automatically solve many problems e.g. ‘unraveling’ arithmetic/logical modifications on input, generating inputs that trigger specific paths, discovering the bounds on given variables and so forth.

I will update this post whenever the REcon videos etc go online. In the meantime I should probably finish at least one of the 5 or so blog posts in a semi-complete state 😛

Finding use-after-free bugs with static analysis

seanhn7 Comments

Earlier this year I had a lot of fun using run-time instrumentation and analysis to tackle a variety of program analysis problems. In doing so I became curious about static solutions to the common problems encountered during dynamic analysis. One of the most obvious issues is that you can only examine those paths that you can execute and thus you need to find some way to drive a program through different paths before you can do any kind of analysis. The flip side of that is that you are guaranteed that any path you analyse is valid and so false positives in that regard are avoided. With those experiences in mind I decided to try my hand at purely static analysis recently (recently as in August, I suck at finding time to document stuff apparently). Static analysis has a large variety of sources of error and annoyances of its own but for certain bug classes it seemed like a purely static approach could find some interesting results with a tolerable level of false positives.

Before I started I considered a few different bug classes in terms of the strengths/weaknesses of static analysis. Certain types of vulnerabilities that depend on the values in registers/memory locations are probably best avoided unless you have the time to either implement a hell of theoretical ideas that can limit the innaccuracy or have the time to sift through thousands of false positives. The bug classes I decided to focus on were those that could generally be reduced to deviations from expected orderings of ‘events’ on a path. Such bug classes include use of memory before initialisation, unchecked use of return values from functions, use after X vulnerabilities (where X is an API call that marks an argument as supposedly unusable e.g. free() or fclose()) and incorrectly ordered sequences of system calls. Eventually I settled on looking for use-after-free vulnerabilities, although the code built to do that works for almost all the mentioned bug classes with a little extending.

(Before continuing I should mention exactly what assumptions and bounds I put on the work I wanted to do. Firstly, I decided to do path insensitive analysis – that is I considered all paths through a control flow graph regardless of whether the path condition is satisfiable or not. To do otherwise would have been extra work and for the vulnerability classes I was considering it didn’t turn out to be a big problem.

Secondly, I decided to do data flow analysis over both registers and memory locations. Some static dataflow analysis (I think binaudit) only considers registers, but in my opinion that misses out on a lot of useful information available at practically zero cost. For instance, if we are doing taint analysis and eax is tainted then after mov [ecx+44], eax; I consider the abstract location denoted by the literal [ecx+44] to also be tainted. It remains in the tainted set until the ecx register is untainted but up until that point it is usable as a source of information.

Thirdly, this project was basically just to give me a taste of the practical side of static analysis so spending a month implementing dataflow analysis for the entire x86 instruction set was out of the question. As a result I implemented the data flow analysis for a small subset of the instruction set I considered to be most relevant to the bug classes considered and wrote a conservative default for all other instructions. That is, for any instructions not specifically considered I make an attempt to guess only their destination operand. The effective result of this is that for such instructions the destination will be removed from whatever analysis I’m doing. This potentially introduces false negatives but also frees up about a month of my life. 😉

Fourthly, when considering loops I only expanded them for one iteration. I haven’t thought too much about the implications of this as there didn’t seem to be a better method without investing time into implementing a bounded loop unwinding technique. It would seem like it might introduce false positives but in my testing I did not encounter anything that could be directly traced back to this weakness. It’s hard to tell if that was due to my small test set, the characteristics of the vulnerabilities I was considering or that my conservative data flow analysis hid the potential false positives.

Fifthly (at this point I’m wishing I’d used 1, 2, 3…), I inititally aimed at intraprocedural analysis and then tacked on some interprocedural fun at the end. I’m quite happy with how my interprocedural hackery worked out but there are probably better (and more time consuming) ways to do it.)

Finding equivalent variables

When doing static analysis you can essentially start at any address that suits the problem at hand. This allows us to divide our algorithm for finding use-after-free bugs into two parts (well three actually, but more about that later). The first part of the algorithm is to decide at a free call what memory locations and registers we want to consider free’d. We want to know all variables that contain pointers to the memory location about to be free’d so that we can consider a use of any of these variables to be a bug.

The most common theoretical framework for this problem is called use-def analysis and is common in compiler theory. In such an analysis we take a variable use (e.g. the push of whatever variable is to be free’d) and compute all its definitions at that point by traversing backwards over all paths to that point. We then want to apply this function recursively over all the definition variables we have found, treating them as uses. By modifying the standard use-def algorithm we can do this to find all variables equivalent to the free’d variable.

In my implementation as I traverse the paths backwards from a free call to find definitions I maintain a list of all locations that are used as destination operands in instructions i.e. they are rewritten before the free call. I will refere to this as the clearedVars list. So, if we are looking for the definition of a variable x and it is found at an instruction mov x, y; we know y is equivalent to the free’d variable if and only if y is not a member of clearedVars. Regardless of whether y is in clearedVars or not we then apply our use-def algorithm to find its definitions with the same considerations. This iterative approach is continued until all paths leading to the free call have been analysed and we are left with a set of variables equivalent to the argument to free.

The following snippet of Python code will hopefully help the explanation. It shows the logic applied to the destination operand of a mov instruction.

if dst in state['needDefList']:
    src = insDataFlow.getSrcFor(dst)
    state['needDefList'].append(src)
                    
    if src not in state['clearedVars']:
        if src not in self.equivVarList:
            self.equivVarList.append(src)
    
    state['needDefList'].remove(dst)
    state['clearedVars'].append(dst)

When finding the set of equivalent variables we can generally avoid many sources of false positives in static analysis by accepting false negatives. The main source of false positives I encountered (that weren’t caused by my lack of coding talent) derived from considering paths with unsatisfiable conditions.

So at this point we have an algorithm for computing a set of equivalent variables given a starting point and a source variable. In case it isn’t obvious, I should point out that the equivalent variables along each path should be stored separately. Otherwise it becomes an avoidable source of false positives in the next part of our algorithm.

Finding use-after-free instances

Most of the work for this algorithm is in the previous stage. Once we have computed the equivalent variables per backwards path we are ready to look for uses of these variables in an unsafe context. We also use the data flow information from each instruction to add/remove variables from the set of locations we consider to hold pointers to free’d memory.

For use-after-free vulnerabilities I considered unsafe use to be any instruction that used the free’d pointer in the computation of a memory address. (I also extended eventually this definition to include any instruction that pushed a free’d pointer to the stack). Checking for such a condition is relatively simple. For each instruction we just iterate over all base registers used in computing the pointer and determine if it is in the set of variables we know to hold free’d pointers or not.

def checkInsForFreeVarUse(self, ea, dst, src, state):
    for op in (dst, src):
        if isinstance(op, TaintLoc_MEMREF_REGS):
            # Usage e.g. mov [ebp+10], eax; and ebp is a free'd var
            for usedReg in op.regs:
                if usedReg in state['freedVars']:
                    self.b00m(ea, usedReg)

In my code the TaintLoc_MEMREF_REGS class represents an operand that is a memory location constructed using at least one register. The objects src and dst are the source and destination operands for a given instruction (a single source and destination suffices for the instructions instrumented in this case).

That is basically the bones of an algorithm that can operate within the bounds of any function containing a call to free; this is useful in its own right but as I thought about it I began to consider cases where a function may free one of its arguments. This could be a problem in two ways: 1) The programmer using the API call is unaware of this functionality, or forgets, or 2) The function should not free the argument and that it does is a flaw in its implementation. The latter case is more interesting in my opinion but the same approach will detect both.

Function aliases and interprocedural analysis

There is probably some other name for what I’m about to describe but let’s call it a ‘function alias’ for now. True interprocedural analysis of a function f containing a call to free would involve relatively complex analysis of the relationship between non-local variables in f and the variables defined at the call sites of f. Doing this properly is non-trivial but we can perform a more limited analysis with much less effort.

The type of interprocedural analysis I implemented begins with searching for aliases to the API call that we are using as the starting point for our algorithms. For use-after-free bugs this is the free function. Let us consider this trigger function as a tuple (f, n), where f is the function in question and n is the argument we consider to be free’d or closed or whatever the action we are interested in happens to be. An alias for a function (f, n) is then a function (g, m) such that calling the function g with the variable x as argument m results in a call to f with x as argument n. If we are provided with one or more aliases for (f, n) we can then apply the exact same analysis algorithm as described in the previous sections to find interprocedural bugs.

The question then becomes how do we build such a list? The answer is pretty simple at a high level – say we are in a function g and analysing a call to the function f that free’s its nth argument. Our first algorithm will build the set of variables equivalent to the nth argument to f, let’s call it E. If any of g‘s arguments are in this set then we know (g, m) is an alias for (f, n) where m is the index of that variable. The only tricky part of this is tracking the function arguments to g. IDA takes care of this for us and renames memory locations automatically using an identifier similar to arg_X but if using another framework you may have to do that yourself. (This turns out to be trickier than you might think, a description of how the simplex method is used in IDA can be found here.)

Righty, so at this point we can take any function and compute its aliases. For maximum fun we apply this recursively to find aliases for aliases and so on, applying our basic analysis algorithms to each discovered alias in turn.

That basically sums up the details of my approach. I used it to look for use-after-free bugs but with varying amounts of effort it could be changed to look for all sorts of fun stuff.

Testing

I tested my implementation (~850 lines of Python using IDAPython as a framework) on libxml2, which has a history of use-after-free bugs, Clam Antivirus, which has a history of sucking and TightVNC, because the name makes me giggle.

The following table summarises the results of my rather brief and unscientific testing.

Analysis results
Analysis results

Both libxml2 and Clam AV came up good for a few bugs each and multiple aliases for free. Some of these aliases were obviously on purpose with names like cl_engine_free, whereas others were more difficult to determine. All three results found in Clam AV were as a result of analysis on an alias function so it is possible that this function has unintended side effects. For libxml2 the bugs were split, two resulting from direct calls to free and two resulting from a call to an alias function. Despite its giggle inducing name, TightVNC showed no bugs and, disappointingly, not even an alias to free. For both libxml2 and Clam AV the false positives were as a result of paths with unsatisfiable conditions.

Conclusion

In the above table I’ve purposely used the term ‘bugs’ instead of ‘vulnerabilities’. The reason for this is the same reason that I’ve now moved on to investigating hybrid dynamic/static implementations. Finding a bug using static analysis of the type I have described gets you a location in a binary where some broken coding idiom occurs. This is useful in its own right and all valid bugs detected during my testing are concrete paths leading to use of a dangling pointer.

From an offensive point of view we must consider the issue further though. Without more analysis you have no idea how to trigger this code or even if it is triggerable in a malicious fashion. In fact, as soon as you get over the initial rush of ‘oh look, a shiney new bug’ you quickly realise you have a mountain of work to actual exercise that code, let alone craft an exploit. From a defensive point of view none of this really matters, the code is incorrect regardless and should be fixed but from an exploit writers point of view discovering the bug in this fashion merely puts your shoes on. You still have a marthon to run in order to get to an exploit.

Game Over! Thank you for playing Academia

seanhn4 Comments

I’ve recently finished my Msc dissertation, titled “Automatic Generation of Control Flow Hijacking Exploits for Software Vulnerabilities“. A PDF copy of it is available here should you feel the need to trawl through 110 or so pages of prose, algorithms, diagrams and general ramblings. The abstract is the following:

Software bugs that result in memory corruption are a common and dangerous feature of systems developed in certain programming languages. Such bugs are security vulnerabilities if they can be leveraged by an attacker to trigger the execution of malicious code. Determining if such a possibility exists is a time consuming process and requires technical expertise in a number of areas. Often the only way to be sure that a bug is in fact exploitable by an attacker is to build a complete exploit. It is this process that we seek to automate. We present a novel algorithm that integrates data-flow analysis and a decision procedure with the aim of automatically building exploits. The exploits we generate are constructed to hijack the control flow of an application and redirect it to malicious code.

Our algorithm is designed to build exploits for three common classes of security vulnerability; stack-based buffer overflows that corrupt a stored instruction pointer, buffer overflows that corrupt a function pointer, and buffer overflows that corrupt the destination address used by instructions that write to memory. For these vulnerability classes we present a system capable of generating functional exploits in the presence of complex arithmetic modification of inputs and arbitrary constraints. Exploits are generated using dynamic data-flow analysis in combination with a decision procedure. To the best of our knowledge the resulting implementation is the first to demonstrate exploit generation using such techniques. We illustrate its effectiveness on a number of benchmarks including a vulnerability in a large, real-world server application.

The implementation of the described system is approx. 7000 lines of C++. I probably won’t be releasing the code as I’m fairly sure I signed over my soul (and anything I might create) to the University earlier in the year. The two core components are a data-flow/taint analysis library and higher level library that uses the previous API to perform data-flow/taint analysis over x86 instructions (as given to us by Pin). Both of these components are useful in their own right so I think I’m going to do a full rewrite (with added GUI + DB) and open source the code in the next couple of months. Hopefully they’ll prove useful for others working on dynamic analysis problems.